
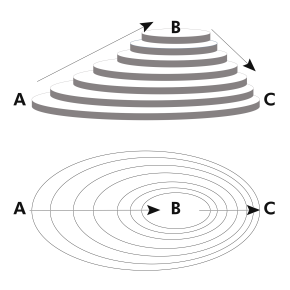
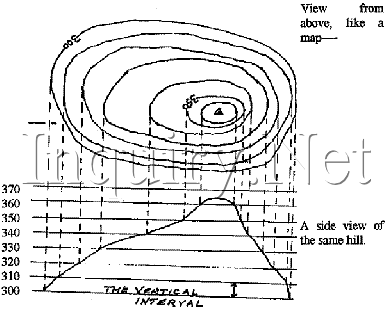
This is not a problem, merely an exact contouring of the data. This can occur when the raster values are integers and they fall exactly on a contour. Occasionally, contours may be created that have square or blocky outlines, appearing to follow raster cell boundaries. These are all valid engineering-quality interpretations of the surface that cartographers typically modify for aesthetic purposes. Branching contours can occur in cases of intersecting ridges that fall exactly on a contour interval. In other cases, the contours may pass so close to one another that they appear to intersect. Crossing contours can occur in saddle regions that lie exactly on a contour interval. Occasionally, engineering-quality contours may cross, appear to intersect, or form an unclosed branching line. A large cell size may result in coarse, blocky contours. The size of the raster cells used affects the appearance of the output contours. Overall contour accuracy depends on how well the data used to create the input raster represents the actual surface. The contour tools produce engineering-quality contours, representing an exact interpretation of the raster surface. The contour attribute table contains an elevation attribute for each contour polyline. They correspond with the areas of higher elevation (in white on the input elevation dataset). The areas where the contours are closer together indicate the steeper locations. The example below shows an input elevation dataset and the output contour dataset. Contours are also a useful surface representation, because they allow you to simultaneously visualize flat and steep areas (distance between contours) and ridges and valleys (converging and diverging polylines). Why create contours?īy following the polyline of a particular contour, you can identify which locations have the same value. The contour creation tools, Contour, Contour List and Contour with Barriers, are used to create a polyline feature dataset from an input raster. Where the values rise or fall rapidly, the lines are closer together. Where there is little change in a value, the lines are spaced farther apart. The distribution of the contour lines shows how values change across a surface. Some examples are isobars for pressure, isotherms for temperature, and isohyets for precipitation. Contour lines are often generally referred to as isolines but can also have specific terms depending on what is being measured. The line features connect cells of a constant value in the input. Posted in books, mathematics, mir books, mir publishers, soviet | Tagged adjoint operators, angles on a surface, annulet, bilinear functionals, Cartan's divisibility theorem, centroaffine transformations, Complexification of a linear operator, conjugate space, Developables, Diffeomorphisms, dual space, eigenfunctions, eigenvalues, euclidean point spaces, euclidean spaces, Frenet’s formulas, gauss theorem, gradients derivatives, graphs of functions, Grassman algebra, Hamilton’s symbolic vector, hyperplanes, hypersurface, indicatrix of dupin, isometries, jacobi theorem, Kronecker-Capelli theorem, linear operators, Matrix rank theorem, Multiplication of tensors, Multivector rank theorem, multivectors, normal vector, Plücker relations, principal curvatures, projections, projective space, quadratic forms, regular surfaces, self-adjoint operators, skew-Hermitian operators., Skew-symmetric Hermitian operators.Contours are lines that connect locations of equal value in a raster dataset that represents continuous phenomena such as elevation, temperature, precipitation, pollution, or atmospheric pressure.


 0 kommentar(er)
0 kommentar(er)
